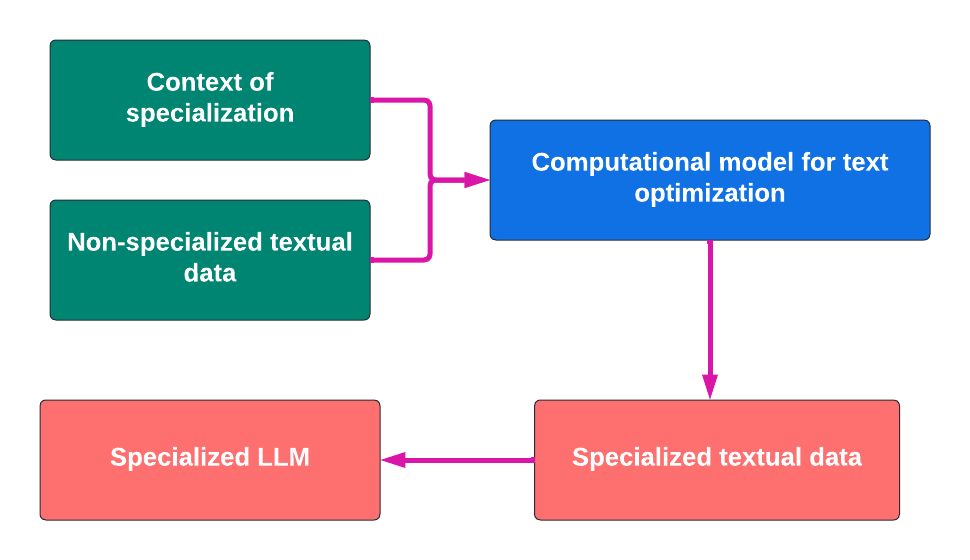
COMPUTATIONAL MODEL FOR TEXT OPTIMIZATION:
Content reduction for improving the semantic perception of information
Author: David MavrodievTask Definition
(Text, Context, Rules) -> Reduced Text
Embeddings Overview
Word embeddings are vector representations that capture a word's meaning based on the contexts in which it appears, positioning similar words close in a high-dimensional space. This allows embeddings to reflect relationships like synonyms, analogies, and usage patterns.
- Word Embeddings Models: Word2Vec, GloVe, FastText, ELMo, BERT etc.
- Sentence Embeddings Models: Average Word Embeddings, InferSent, Universal Sentence Encoder, SBERT, LASER etc.
- Paragraph Embeddings: Average of Sentence Embeddings, Doc2Vec, Hierarchical Attention Networks, Deep Averaging Networks, etc.
Text
In this context, \( T = \{t_1, t_2, \dots, t_n\} \) represents a set of embedding vectors for words, sentences, or paragraphs from the text. Each element \( t_i \) in the set \( T \) is a vector that encodes some linguistic information about a particular word, sentence, or paragraph.
Context
\( C = \{c_1, c_2, \dots, c_m\} \) represents a set of embedding vectors corresponding to context elements. Each element \( c_i \) in the set \( C \) is a vector that encodes some semantic or informational significance about the specific context element, which can be a word, sentence, or paragraph related to a larger text or domain.
Let \( I = \{I_1, I_2, \dots, I_n\} \) represent the weights for each context element, indicating their informational importance. Such weights could be based on the rarity of the elements—rarer elements (words, sentences, paragraphs) typically carry more informational importance because they are less expected and thus contribute more uniquely to the overall meaning.
Similarity Measurement
Between Words, Sentences, and Paragraphs
- Word similarity: Cosine Similarity, Euclidean Distance, Jaccard Similarity, etc.
- Sentence Similarity: Cosine Similarity, Word Mover's Distance (WMD), Semantic Similarity, etc.
- Paragraph Similarity: Average Embedding Similarity, Doc2Vec Similarity, etc.
The weighted similarity \( V \) between context elements and text elements is: \[ V = \sum_{i=1}^{m} I_i \sum_{j=1}^{n} \text{sim}(c_i, t_j) \]
Understanding Measurement
Let \( S \) be the understanding measurement, defined as the ratio between the initial similarity \( V \) and the similarity after text reduction \( V_{\text{reduced}} \).
The understanding measurement \( S \) is the ratio between these two similarity values: \[ S = \frac{V_{\text{reduced}}}{V} \leq 1 \]
Quality of Text Reduction
The formula for evaluating the quality of text reduction is:
\[ O = S \times \log_2 \left( \frac{a}{b} \right), \, a < b \]
Where:
- \( S \) is the understanding retained after text reduction.
- \( a \) is the size of the text after reduction.
- \( b \) is the original text size before reduction.
This formula measures the trade-off between reducing text size and retaining understanding. Higher \( O \) values indicate a better balance.
Introducing Rules for Text Reduction
Rules allow you to define allowed ranges for measurements during text reduction. These rules set constraints on how much understanding can be lost or the size of the reduced text.
For example:
- Understanding Rule: Require that at least 90% of the original understanding is retained: \[ S \geq 0.9 \]
- Size Rule: Only consider reduced text versions that are less than 50% of the original size: \[ a \leq 0.5 \times b \]
Combining Rules for Optimal Reduction
By combining rules for understanding and text size, you can control the quality and efficiency of the text reduction process. For example:
- Only allow a maximum 10% loss in understanding (\( S \geq 0.9 \)).
- Ensure that the reduced text is less than 50% of the original size (\( a \leq 0.5 \times b \)).
These rules help guide the search for the most optimal reduced text versions that maintain both meaning and conciseness.
Properties
I. Removing semantically repetitive elements optimizes the content without changing the information.
$$ I_i \cup I_j \neq \emptyset $$
II. The absence of an element that semantically contradicts another improves the comprehension of the content without altering the information.
$$ I_i = I_j^c $$
Definition of optimal text:
- A text consisting of elements that contain different, not identical or mutually exclusive information.
- A text which, if shortened, would suffer in comprehension because the information or part of it would be lost.
Software application 'Textopt'

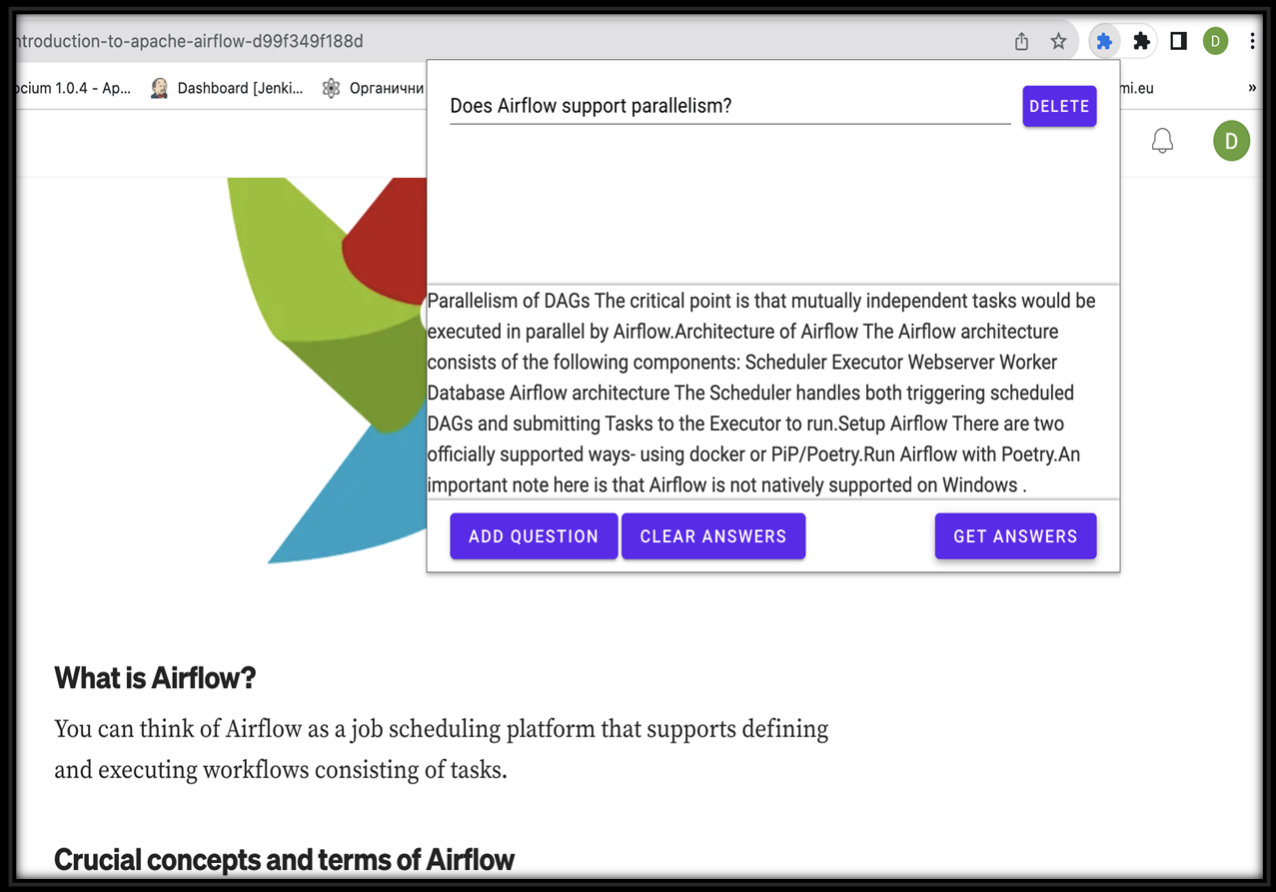
Training specialized language models